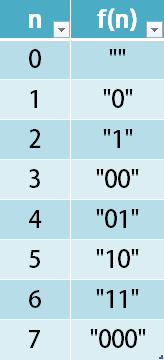
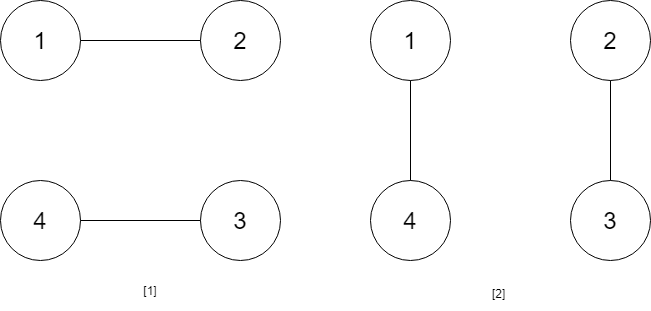
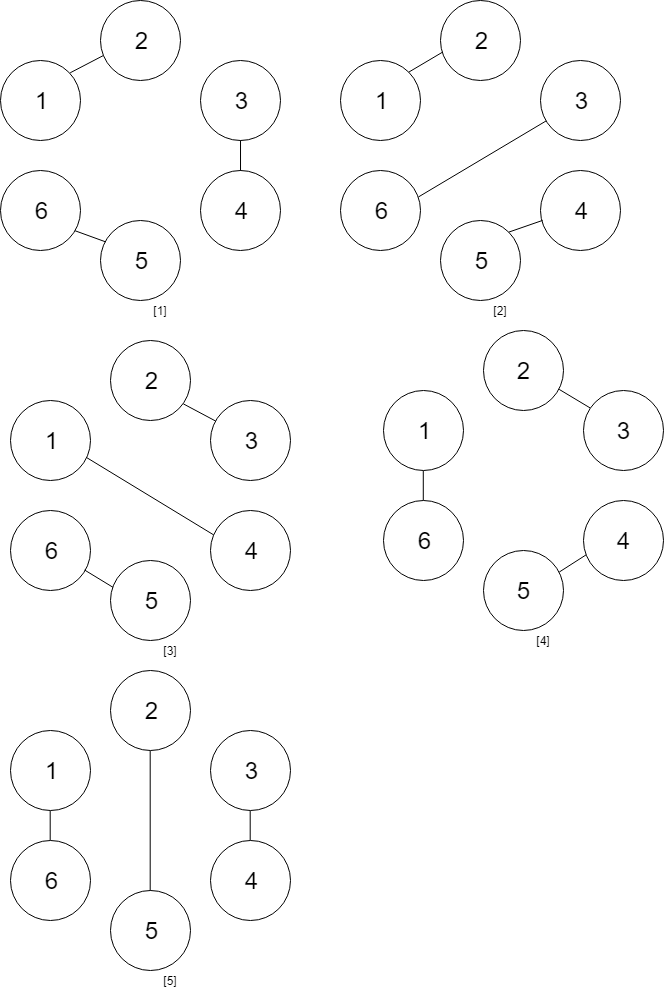
题目描述 给你一个 n 行 m 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。 每次「迁移」操作将会引发下述活动： 位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。 位于 grid[i][m - 1] 的元素将会移动到 grid[i + 1][0]。 位于 grid[n - 1][m - 1] 的元素将会移动到 grid[0][0]。 请你返回 k 次迁移操作后最终得到的 二维网格。 示例 1：
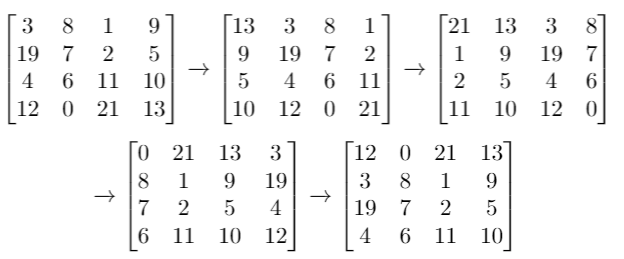
题解1 之前做过一个一维数组元素平移，最后面的移到前面。比赛时首先想到的是先把二维数组转成一维数组，然后平移元素。注意平移周期为数组长度。可以先对平移长度取模。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : vector<vector<int >> shiftGrid (vector<vector<int >>& grid, int k) { vector<int >tmp; int rows = grid.size (), cols = grid[0 ].size (); for (int i = 0 ; i < grid.size (); ++i){ for (int j = 0 ; j < grid[i].size (); ++j){ tmp.push_back (grid[i][j]); } } int len = tmp.size (); k = k % len; for (int i = 0 ; i < len; ++i){ grid[i / cols][i % cols] = tmp[(i - k + len) % len]; } return grid; } };
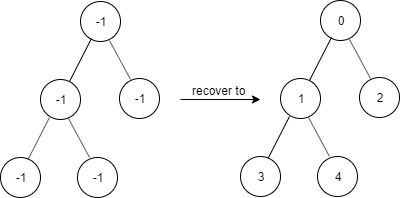
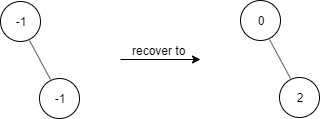
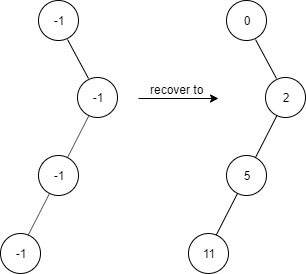
题目描述 给出一个满足下述规则的二叉树： root.val == 0 如果 treeNode.val == x 且 treeNode.left != null，那么 treeNode.left.val == 2 * x + 1 如果 treeNode.val == x 且 treeNode.right != null，那么 treeNode.right.val == 2 * x + 2 现在这个二叉树受到「污染」，所有的 treeNode.val 都变成了 -1。 请你先还原二叉树，然后实现 FindElements 类： FindElements(TreeNode* root) 用受污染的二叉树初始化对象，你需要先把它还原。 bool find(int target) 判断目标值 target 是否存在于还原后的二叉树中并返回结果。 示例 1：
题解1 题目大意是已经给出二叉树的结构，但是结点值不正确，首先根据给定的规则，对二叉树节点重新赋值。然后写出find函数。 对于二叉树的构建及find函数常见的方法是递归的方式，但是后来我发现find的传入参数不是没有root。实现有点麻烦，后来用的是队列实现的。类似于BFS
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class FindElements {public : TreeNode *res; FindElements (TreeNode* root) { res = root; if (res == NULL ){ return ; } queue<TreeNode*>que; TreeNode* frt; res->val = 0 ; que.push (res); while (!que.empty ()){ frt = que.front (); que.pop (); if (frt->left != NULL ){ frt->left->val = frt->val * 2 + 1 ; que.push (frt->left); } if (frt->right != NULL ){ frt->right->val = frt->val * 2 + 2 ; que.push (frt->right); } } } bool find (int target) if (res == NULL ){ return false ; } else { queue<TreeNode*>que; TreeNode* frt; que.push (res); while (!que.empty ()){ frt = que.front (); que.pop (); if (frt->val == target){ return true ; } if (frt->left != NULL ){ que.push (frt->left); } if (frt->right != NULL ){ que.push (frt->right); } } return false ; } } };
题目描述 给你一个整数数组 nums，请你找出并返回能被三整除的元素最大和。 示例 1： 输入：nums = [3,6,5,1,8] 输出：18 解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。 示例 2： 输入：nums = [4] 输出：0 解释：4 不能被 3 整除，所以无法选出数字，返回 0。 示例 3： 输入：nums = [1,2,3,4,4] 输出：12 解释：选出数字 1, 3, 4 以及 4，它们的和是 12（可被 3 整除的最大和）。 提示： 1 <= nums.length <= 4 * 10^4 1 <= nums[i] <= 10^4
题解1 这个题比赛的时候，思路没理清，导致写出来的代码bug多，赛后想了感觉很简单。 1. 所有元素排序 2. 求所有元素之和对3的余数res，期间各存下余数为1和余数为2的最小的2个数（4个数） 3. res = 0的话，被三整除的最大和为元素和。res=1的话需要去除1个余数为1的数或2个余数为2的数，需要比较一个，选择和大的一个。res=2的话需要去除2个余数为1的数或1个余数为2的数，同样比较取和较大的一种方案
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : int maxSumDivThree (vector<int >& nums) sort (nums.begin (), nums.end ()); int sum = 0 , mod = 0 , len = nums.size (), res; vector<int >v1, v2; for (int i = 0 ; i < len; ++i){ sum = sum + nums[i]; mod = (mod + nums[i]) % 3 ; if (v1.size () < 2 && nums[i] % 3 == 1 ){ v1.push_back (nums[i]); } else if (v2.size () < 2 && nums[i] % 3 == 2 ){ v2.push_back (nums[i]); } } if (mod == 0 ){ res = sum; } else if (mod == 1 ){ int num1 = sum - (v1.size () > 0 ?v1[0 ]:sum); int num2 = sum - (v2.size () > 1 ?v2[0 ] + v2[1 ]:sum); res = max (num1, num2); } else { int num1 = sum - (v1.size () > 1 ?v1[0 ] + v1[1 ]:sum); int num2 = sum - (v2.size () > 0 ?v2[0 ]:sum); res = max (num1, num2); } return res; } };
题目描述 「推箱子」是一款风靡全球的益智小游戏，玩家需要将箱子推到仓库中的目标位置。 游戏地图用大小为 n * m 的网格 grid 表示，其中每个元素可以是墙、地板或者是箱子。 现在你将作为玩家参与游戏，按规则将箱子 ‘B’ 移动到目标位置 ‘T’ ： 玩家用字符 ‘S’ 表示，只要他在地板上，就可以在网格中向上、下、左、右四个方向移动。 地板用字符 ‘.’ 表示，意味着可以自由行走。 墙用字符 ‘#’ 表示，意味着障碍物，不能通行。 箱子仅有一个，用字符 ‘B’ 表示。相应地，网格上有一个目标位置 ‘T’。 玩家需要站在箱子旁边，然后沿着箱子的方向进行移动，此时箱子会被移动到相邻的地板单元格。记作一次「推动」。 玩家无法越过箱子。 返回将箱子推到目标位置的最小 推动 次数，如果无法做到，请返回 -1。 示例 1：
题解1 参照题解 如果只有箱子没有人，只是将箱子移到目标位置，就是常见的BFS问题。而这个题有两个对象，箱子和人，要保证箱子能被推到目标位置。加入队列的信息除了箱子的坐标还有人的坐标，随着人的移动来判断人是否能走到箱子的位置，能表示箱子移动，步数加1；否则只是人的位置发生移动，此时步数并未增加。此外，标记对象也发生改变，以前只是箱子这个二元组，现在变成了人和箱子这个四元组。因为人移动带来的步数并不一定增长，这里需要用到优先队列，每次选取步数最小的来移动。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 struct cmp { bool operator () (vector<int >v1, vector<int >v2) return v1[0 ] > v2[0 ]; } }; int dir[4 ][2 ] = {{0 , 1 }, {1 , 0 }, {0 , -1 }, {-1 , 0 }};class Solution {public : int minPushBox (vector<vector<char >>& grid) set<vector<int > >mark; int rows = grid.size (), cols = grid[0 ].size (); int x1, x2, y1, y2, x3, y3, next_x, next_y, dist; vector<int >v; priority_queue<vector<int >, vector<vector<int >>, cmp>que; for (int i = 0 ; i < rows; ++i){ for (int j = 0 ; j < cols; ++j){ if (grid[i][j] == 'S' ){ x1 = i; y1 = j; } else if (grid[i][j] == 'B' ){ x2 = i; y2 = j; } else if (grid[i][j] == 'T' ){ x3 = i; y3 = j; } } } que.push ({0 , x1, y1, x2, y2}); mark.insert ({x1, y1, x2, y2}); while (!que.empty ()){ v = que.top (); que.pop (); if (v[3 ] == x3 && v[4 ] == y3){ return v[0 ]; } for (int i = 0 ; i < 4 ; ++i){ x1 = v[1 ] + dir[i][0 ]; y1 = v[2 ] + dir[i][1 ]; dist = v[0 ]; if (x1 < 0 x1 >= rows y1 < 0 y1 >= cols){ continue ; } if (grid[x1][y1] != '#' ){ if (x1 == v[3 ] && y1 == v[4 ]){ x2 = v[3 ] + dir[i][0 ]; y2 = v[4 ] + dir[i][1 ]; if (x2 >= 0 && x2 < rows && y2 >= 0 && y2 < cols && grid[x2][y2] != '#' ){ if (mark.find ({x1, y1, x2, y2}) == mark.end ()){ mark.insert ({x1, y1, x2, y2}); que.push ({dist + 1 , x1, y1, x2, y2}); } } } else { if (mark.find ({x1, y1, v[3 ], v[4 ]}) == mark.end ()){ mark.insert ({x1, y1, v[3 ], v[4 ]}); que.push ({dist, x1, y1, v[3 ], v[4 ]}); } } } } } return -1 ; } };
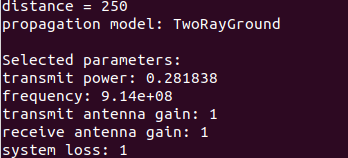执行命令
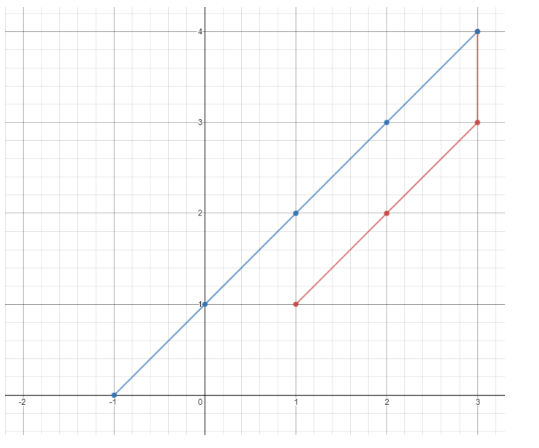输入：points = [[1,1],[3,4],[-1,0]] 输出：7 解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0] 从 [1,1] 到 [3,4] 需要 3 秒 从 [3,4] 到 [-1,0] 需要 4 秒 一共需要 7 秒 示例 2： 输入：points = [[3,2],[-2,2]] 输出：5 提示： points.length == n 1 <= n <= 100 points[i].length == 2 -1000 <= points[i][0], points[i][1] <= 1000
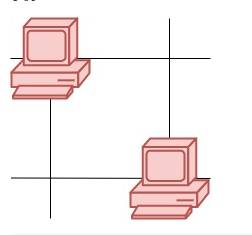输入：grid = [[1,0],[0,1]] 输出：0 解释：没有一台服务器能与其他服务器进行通信。 示例 2： 
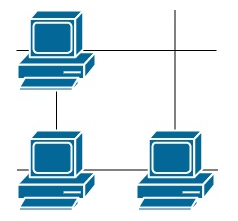输入：grid = [[1,0],[1,1]] 输出：3 解释：所有这些服务器都至少可以与一台别的服务器进行通信。 示例 3： 
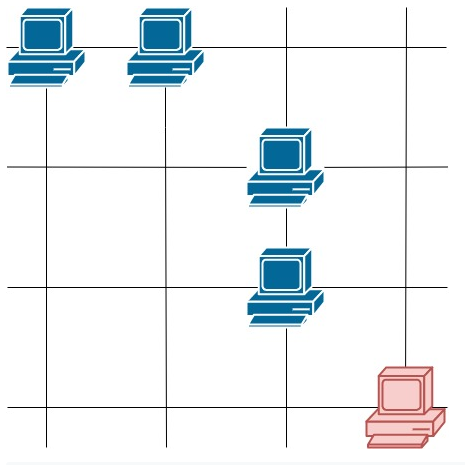输入：grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]] 输出：4 解释：第一行的两台服务器互相通信，第三列的两台服务器互相通信，但右下角的服务器无法与其他服务器通信。 提示： m == grid.length n == grid[i].length 1 <= m <= 250 1 <= n <= 250 grid[i][j] == 0 or 1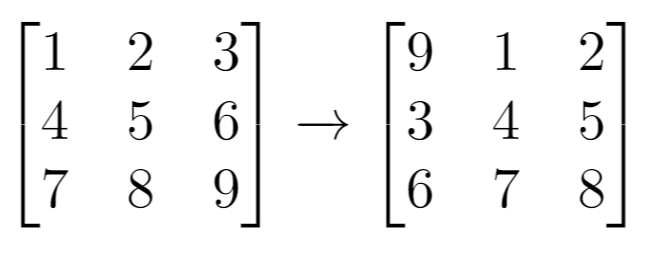
输入：grid = [[“#”,”#”,”#”,”#”,”#”,”#”], [“#”,”T”,”#”,”#”,”#”,”#”], [“#”,”.”,”.”,”B”,”.”,”#”], [“#”,”.”,”#”,”#”,”.”,”#”], [“#”,”.”,”.”,”.”,”S”,”#”], [“#”,”#”,”#”,”#”,”#”,”#”]] 输出：3 解释：我们只需要返回推箱子的次数。 示例 2： 输入：grid = [[“#”,”#”,”#”,”#”,”#”,”#”], [“#”,”T”,”#”,”#”,”#”,”#”], [“#”,”.”,”.”,”B”,”.”,”#”], [“#”,”#”,”#”,”#”,”.”,”#”], [“#”,”.”,”.”,”.”,”S”,”#”], [“#”,”#”,”#”,”#”,”#”,”#”]] 输出：-1 示例 3： 输入：grid = [[“#”,”#”,”#”,”#”,”#”,”#”], [“#”,”T”,”.”,”.”,”#”,”#”], [“#”,”.”,”#”,”B”,”.”,”#”], [“#”,”.”,”.”,”.”,”.”,”#”], [“#”,”.”,”.”,”.”,”S”,”#”], [“#”,”#”,”#”,”#”,”#”,”#”]] 输出：5 解释：向下、向左、向左、向上再向上。 示例 4： 输入：grid = [[“#”,”#”,”#”,”#”,”#”,”#”,”#”], [“#”,”S”,”#”,”.”,”B”,”T”,”#”], [“#”,”#”,”#”,”#”,”#”,”#”,”#”]] 输出：-1 提示： 1 <= grid.length <= 20 1 <= grid[i].length <= 20 grid 仅包含字符 ‘.’, ‘#’, ‘S’ , ‘T’, 以及 ‘B’。 grid 中 ‘S’, ‘B’ 和 ‘T’ 各只能出现一个。
