题目描述
给你一个整数 n，请你返回 任意 一个由 n 个 各不相同 的整数组成的数组，并且这 n 个数相加和为 0 。 示例 1： 输入：n = 5 输出：[-7,-1,1,3,4] 解释：这些数组也是正确的 [-5,-1,1,2,3]，[-3,-1,2,-2,4]。 示例 2： 输入：n = 3 输出：[-1,0,1] 示例 3： 输入：n = 1 输出：[0] 提示： 1 <= n <= 1000
题解1
产生n个不同的数字和为0的方式有很多种，可以对称产生0左右两边的数。具体 如果$n = 2 m$，则结果为：$-m, -(m - 1), \dots, -1, 1, \dots, m - 1, m$。 如果$n = 2 m + 1$，则结果为：$-m, -(m - 1), \dots, -1, 0，1, \dots, m - 1, m$。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
vector<int> sumZero(int n) {
vector<int>res;
if(n & 1 == 1){
res.push_back(0);
}
for(int i = 1; i <= n >> 1; ++i){
res.push_back(i);
res.push_back(-i);
}
return res;
}
};
|
题目描述
给你 root1 和 root2 这两棵二叉搜索树。 请你返回一个列表，其中包含 两棵树 中的所有整数并按 升序 排序。. 示例 1：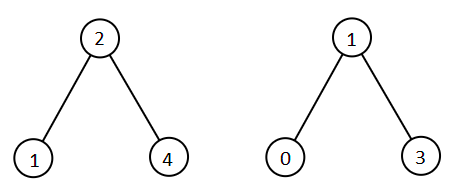 
输入：root1 = [2,1,4], root2 = [1,0,3] 输出：[0,1,1,2,3,4] 示例 2： 输入：root1 = [0,-10,10], root2 = [5,1,7,0,2] 输出：[-10,0,0,1,2,5,7,10] 示例 3： 输入：root1 = [], root2 = [5,1,7,0,2] 输出：[0,1,2,5,7] 示例 4： 输入：root1 = [0,-10,10], root2 = [] 输出：[-10,0,10] 示例 5： 
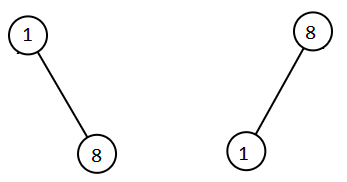输入：root1 = [1,null,8], root2 = [8,1] 输出：[1,1,8,8] 提示： 每棵树最多有 5000 个节点。 每个节点的值在 [-10^5, 10^5] 之间。
题解1
对于二叉搜索树，中序遍历可以得到有序的序列。分别对两棵二叉搜索树中序遍历，然后再对结果进行归并排序。 但比赛为了求速度，直接将结果用sort排序。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
void inorder(TreeNode* root, vector<int>& res){
if(root == NULL){
return;
}
inorder(root->left, res);
res.push_back(root->val);
inorder(root->right, res);
}
class Solution {
public:
vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
vector<int>res1;
inorder(root1, res1);
inorder(root2, res1);
sort(res1.begin(), res1.end());
return res1;
}
};
|
题目描述
这里有一个非负整数数组 arr，你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时，你可以跳到 i + arr[i] 或者 i - arr[i]。 请你判断自己是否能够跳到对应元素值为 0 的 任意 下标处。 注意，不管是什么情况下，你都无法跳到数组之外。 示例 1： 输入：arr = [4,2,3,0,3,1,2], start = 5 输出：true 解释： 到达值为 0 的下标 3 有以下可能方案： 下标 5 -> 下标 4 -> 下标 1 -> 下标 3 下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3 示例 2： 输入：arr = [4,2,3,0,3,1,2], start = 0 输出：true 解释： 到达值为 0 的下标 3 有以下可能方案： 下标 0 -> 下标 4 -> 下标 1 -> 下标 3 示例 3 输入：arr = [3,0,2,1,2], start = 2 输出：false 解释：无法到达值为 0 的下标 1 处。 提示： 1 <= arr.length <= 5 * 10^4 0 <= arr[i] < arr.length 0 <= start < arr.length
题解1
BFS，判断能否从起始下标到达值为0的下标位置
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public:
bool canReach(vector<int>& arr, int start) {
vector<int>target;
int len = arr.size(), frt;
bool flag = false, res = false;
vector<int>mark(len, 0);
vector<int>mark1(len, 0);
for(int i = 0; i < arr.size(); ++i){
if(arr[i] == 0){
mark[i] = 1;
flag = true;
}
}
if(!flag){
res = false;
}
else{
queue<int>que;
que.push(start);
mark1[start] = 1;
while(!que.empty()){
frt = que.front();
que.pop();
if(mark[frt]){
res = true;
break;
}
if(frt + arr[frt] < len && !mark1[frt + arr[frt]]){
que.push(frt + arr[frt]);
mark1[frt + arr[frt]] = 1;
}
if(frt - arr[frt] >= 0 && !mark1[frt - arr[frt]]){
que.push(frt - arr[frt]);
mark1[frt - arr[frt]] = 1;
}
}
}
return res;
}
};
|
题目描述
给你一个方程，左边用 words 表示，右边用 result 表示。 你需要根据以下规则检查方程是否可解： 每个字符都会被解码成一位数字（0 - 9）。 每对不同的字符必须映射到不同的数字。 每个 words[i] 和 result 都会被解码成一个没有前导零的数字。 左侧数字之和（words）等于右侧数字（result）。 如果方程可解，返回 True，否则返回 False。 示例 1： 输入：words = [“SEND”,”MORE”], result = “MONEY” 输出：true 解释：映射 ‘S’-> 9, ‘E’->5, ‘N’->6, ‘D’->7, ‘M’->1, ‘O’->0, ‘R’->8, ‘Y’->’2’ 所以 “SEND” + “MORE” = “MONEY” , 9567 + 1085 = 10652 示例 2： 输入：words = [“SIX”,”SEVEN”,”SEVEN”], result = “TWENTY” 输出：true 解释：映射 ‘S’-> 6, ‘I’->5, ‘X’->0, ‘E’->8, ‘V’->7, ‘N’->2, ‘T’->1, ‘W’->’3’, ‘Y’->4 所以 “SIX” + “SEVEN” + “SEVEN” = “TWENTY” , 650 + 68782 + 68782 = 138214 示例 3： 输入：words = [“THIS”,”IS”,”TOO”], result = “FUNNY” 输出：true 示例 4： 输入：words = [“LEET”,”CODE”], result = “POINT” 输出：false 提示： 2 <= words.length <= 5 1 <= words[i].length, results.length <= 7 words[i], result 只含有大写英文字母 表达式中使用的不同字符数最大为 10
题解1
因为表达式中使用的不同字符数最大为10，字符的取值0-9（值不能相同）最多为$10!$种情况。思路如下： 首先将不重复的字符统计出来，然后用next_permutation产生不同的取值，判断是否符合情况。 这种暴力方式会超时，因为next_permutation产生取值的时间需要o(n)时间，并且包含重复的情况。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
bool deal(vector<string>& words, string& result, unordered_map<char, int>& myMap){
for(int i = 0; i < words.size(); ++i){
if(words[i].size() > 1 && myMap[words[i][0]] == 0){
return false;
}
}
if(result.size() > 1 && myMap[result[0]] == 0){
return false;
}
int lSum = 0, rSum = 0, num = 0;
for(auto word:words){
num = 0;
for(auto ch:word){
num = num * 10 + myMap[ch];
}
lSum += num;
}
for(auto ch:result){
rSum = rSum * 10 + myMap[ch];
}
return lSum == rSum;
}
class Solution {
public:
bool isSolvable(vector<string>& words, string result) {
int len;
unordered_map<char, int>myMap;
string str;
int flag = false;
int arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
for(auto word:words){
for(auto ch:word){
if(myMap.find(ch) == myMap.end()){
str.push_back(ch);
myMap[ch] = 0;
}
}
}
len = str.size();
do{
for(int i = 0; i < len; ++i){
myMap[str[i]] = arr[i];
}
if(deal(words, result, myMap)){
flag = true;
break;
}
}while(next_permutation(arr, arr + 10));
return flag;
}
};
|
题解2
用dfs来代替next_permutation，不会产生重复的情况。加入前导0的标记并将map换成数组。
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| vector<int>myMap(26, 0);
vector<bool>mark(26, 0);
string str;
bool res = false;
bool deal(vector<string>& words, string& result){
int lSum = 0, rSum = 0, num = 0;
for(auto word:words){
num = 0;
for(auto ch:word){
num = num * 10 + myMap[ch - 'A'];
}
lSum += num;
}
for(auto ch:result){
rSum = rSum * 10 + myMap[ch - 'A'];
}
return lSum == rSum;
}
void dfs(vector<string>& words, string& result, int pos, int used){
if(res){
return;
}
if(pos == str.size()){
if(deal(words, result)){
res = true;
}
return;
}
for(int i = 0; i < 10; ++i){
if((mark[str[pos] - 'A'] && i == 0) used >> i & 1) continue;
myMap[str[pos] - 'A'] = i;
dfs(words, result, pos + 1, used 1 << i);
}
}
class Solution {
public:
bool isSolvable(vector<string>& words, string result) {
int len;
myMap.clear();
str.clear();
res = false;
mark.assign(26, 0);
myMap.assign(26, 0);
for(auto word:words){
mark[word[0] - 'A'] = 1;
for(auto ch:word){
if(!myMap[ch - 'A']){
str.push_back(ch);
myMap[ch - 'A'] = 1;
}
}
}
mark[result[0] - 'A'] = 1;
for(auto ch:result){
if(!myMap[ch - 'A']){
str.push_back(ch);
myMap[ch - 'A'] = 1;
}
}
len = str.size();
dfs(words, result, 0, 0);
return res;
}
};
|
题解3
参照圈子
代码3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| vector<char> h;
vector<int> base;
vector<int> coe(26,0);
vector<bool> not_zero(26,false);
bool dfs (int pos,int used, int sum) {
if(pos == h.size()) return sum == 0;
for(int i = 0 ; i < 10 ; i++) {
if(used>>i & 1) continue;
if(i==0 && not_zero[h[pos]-'A']) continue;
if(dfs(pos+1,used 1<<i, sum+i*coe[h[pos]-'A'])) return true;
}
return false;
};
class Solution {
public:
bool isSolvable(vector<string>& words, string result) {
h.clear();
base.clear();
coe.assign(26, 0);
not_zero.assign(26, false);
words.push_back(result);
base.push_back(1);
for(int i = 1 ; i <= 8 ; i++) base.push_back(base.back()*10);
for(int j = 0 ; j < words.size() ; j++) {
string x = words[j];
for(int i = 0 ; i < x.size() ; i++) {
if(i==0) not_zero[x[i]-'A'] = true;
h.push_back(x[i]);
int flag = j==words.size()-1?-1:1;
coe[x[i]-'A'] += flag * base[x.size()-1-i];
}
}
sort(h.begin(),h.end());
h.erase(unique(h.begin(),h.end()),h.end());
return dfs(0,0,0);
}
};
|