计算理论学习笔记（二）
上下文无关文法(CFG)
定义
前面提到的$0^n1^n$可以用上下文无关文法表示如下： $S\rarr 0S1\vert \epsilon$.
设计CFG
CFG的设计很难对于多个简单CFG的合并或者语言本身是DFA都较容易设计。 
有些很难的CFG是在一些基础的CFG上发展来的，所以需要记住一些常见的CFG的形式。 一些常见的CFG表示如图所求. 
乔姆斯基范式
乔姆斯基范式有两个特点：一分为二；终级化. 将任意一个上下文无关文法转为乔姆斯基范式的步骤如下： 1. 引入新的起始变元 2. 删除$\epsilon$规则，相同的只替换一次，不循环替换 3. 去掉单一规则 4. 添加终结符规则 5. 添加新变元，使得所有变量规则都是一分为二 具体可参考65页的例3.7. 乔姆斯基范式有一个很重要的性质，在后面证$A_{CFG}$图灵可判定及多项式时间内判定某个串是否可以派生，都要用到乔姆斯基范式。因为乔姆斯基范式派生任何长为n的串，只需要$2n-1$步。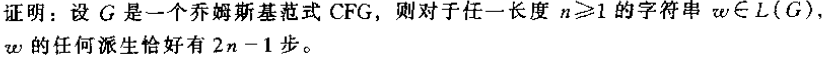 
证明如图所求。 
下推自动机(PDA)
下推自动机相比NFA多了一个栈（可以压入与弹出）。可以进行简单的串的数量的统计。
定义
常见的PDA
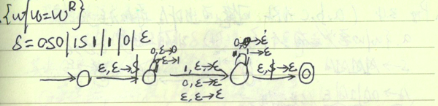
泵引理
与正则语言相同，上下文无关语言也有泵引理。
定义
用泵引理证明非上下文无关语言
“抽进”+“抽出” 
注意：上下文 无关语言对并运算是封闭的，而对交，补，差都不是封闭的.