计算理论学习笔记（三）
图灵机(TM)
有穷自动机与图灵机区别：图灵机在带子上能写能读；读写头即能左移也能右移；带子无限长；进入拒绝和接受状态立即停机。
定义
格局 
图灵可判定：有限步骤内，可知结果是yes或者no. 图灵可识别：有限步骤内，可知结果是yes.对于no的可能进入死循环. 图灵可补识别：有限步骤内，可知结果是no.对于yes的可能进入死循环. 识别语言$0^{2^n}$的图灵机如图.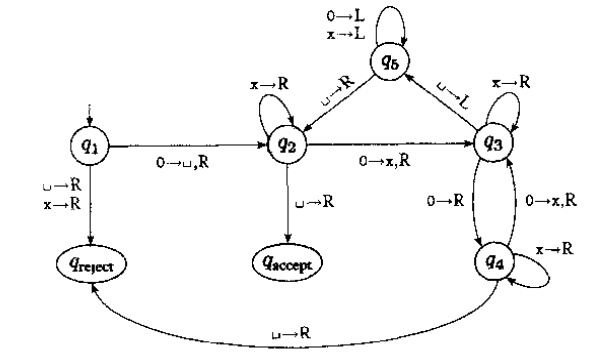 
每次减半，直到1个0结束。中间出现奇数个0且不为1个，则进入拒绝态。
图灵可判定性
$A_{DFA}$显然可判定，因为DFA对于每个输入的串要不进入接受态，要不进入拒绝态。$E_{DFA}$采用的是标记法，类似于图中遍历。因为正则语言对于交，并，补运算都是封闭的，所以$EQ_{DFA}$可以转成$E_{DFA}$，而$ALL_{DFA}$又能转成$EQ_{DFA}$ 
CFG的相关的可判定性问题，很大程度上依赖于乔姆斯基范式。$A_{CFG}$使用乔姆斯基范式能有限步内（2n-1步）判断能否识别某串。$A_{\epsilon CFG}$直接借用$A_{CFG}$可判定的结论，来判断是否能派生$\epsilon$串。$E_CFG}$可判定同样采用标记法，不过是逆向标记。 
证明思路类似于$E_{CFG}$的证明.
可归约性
定义
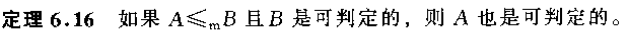
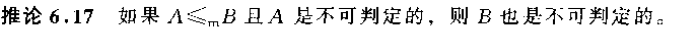
证明$A_{TM}$不可判定，使用的是对角化方法。 
