11. 盛最多水的容器 - 力扣（LeetCode）

发表于 更新于 分类于 阅读次数： Disqus：

题目描述

给定 n 个非负整数 [latex]a_1，a_2，\\cdots, a_n[/latex]，每个数代表坐标中的一个点 [latex](i, a_i)[/latex] 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 [latex](i, a_i)[/latex] 和[latex](i, 0)[/latex]。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 说明：你不能倾斜容器，且 n 的值至少为 2。 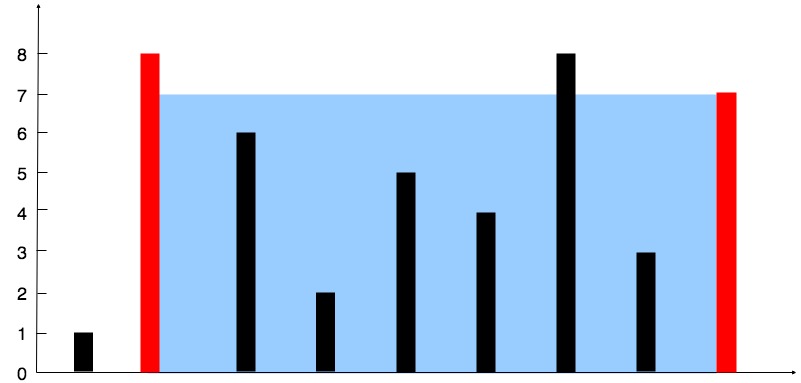示例:

1
2
输入: [1,8,6,2,5,4,8,3,7]
输出: 49

题解

最容易想到的肯定是暴力求解的方法，将所有可能的组合都尝试，然后选取出面积最大的。但是时间复杂度是[latex]o(n^2)[/latex]，运行时间会很长，从执行结果上看，仅击败了5%的用户。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxArea(vector<int>& height) {
        int res = 0, tmpArea = 0;
        for(int i = 0; i <height.size(); ++i){
            for(int j = i + 1; j < height.size(); ++j){
                tmpArea = min(height[i], height[j]) * (j - i);
                if(tmpArea > res){
                    res = tmpArea;
                }
            }
        }
        return res;
    }
};

执行结果

优化

参考官方给出的题解，采用双指针的方法。初始时两指针i与j分别指向数据height的两侧，与x轴构成的容器的面积为: [latex] Area = min(height[i], height[j]) * (j - i)\\\\ [/latex] 然后指向height较小的指针向内侧移动（对i来说，就是增加；对j来说，就是减小），为什么要这做呢？如果较大的指针向内侧移动则[latex] j - i [/latex]的值一定会减小，而[latex] min(height[i], height[j]) [/latex]的值 是小于等于移动之前的min(height[i], height[j])。这样[latex] area [/latex]一定会减小。所以要将较小的指针向内侧移动。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1;
        int resArea = 0, tmpArea;
        while(i < j){
            tmpArea = min(height[i], height[j]) * (j - i);
            if(tmpArea > resArea){
                resArea = tmpArea;
            }
            if(height[i] > height[j]){
                --j;
            }
            else{
                ++i;
            }
        }
        return resArea;
    }
};

执行结果