弗洛伊德的兔子与乌龟(Floyd's Tortoise and the Hare algorithm)

发表于 2020-02-05 更新于 2022-02-13 分类于算法阅读次数： Disqus：

参考资料

算法解读

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。该算法据高德纳称由美国科学家罗伯特·弗洛伊德发明。

引用自维基百科-Floyd判圈算法

问题引入

如何检测一个链表是否有环（循环节），如果有，那么如何确定环的起点以及环的长度。

引用自博客上述问题是一个经典问题，经常会在面试中被问到。我之前在杭州一家网络公司的电话面试中就很不巧的问到，当时是第一次遇到那个问题（毕竟太菜，没有专门准备过算法面试），我思考片刻，问答的是用一个哈希表存储访问的节点的地址，当访问某节点时，发现哈希表中已存在，表明链表中存在环。面试官听了我的回答就反问了我一句：如果链表的环很大，那么哈希表的空间消耗就很大，你的方法并不实用。你能在不消耗额外空间的情况下，找到链表的环吗？当时，想了很久没想到，面试官就说可以这样做，balabala…

算法描述

形象化解释

解决上述问题的方法就是我们常说的快慢指针。乌龟与兔子在一个含环的跑道上（如图所求）进行比赛，乌龟在单位时间内移动一步，而兔子则在单位时间内移动两步，其移动速度是乌龟的两倍。乌龟与兔子同时从A点出发，兔子移动的快先行进入环形跑道，但那以后，一直在转圈。所以如果存在环的话，乌龟总能与兔子相遇（首次相遇在C点），甚至还能跑到兔子前面:joy:。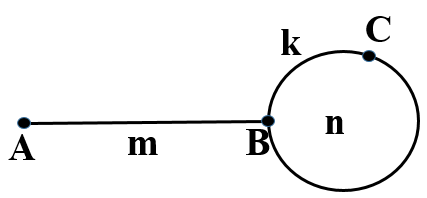

判断是否有环

定义两个指针p1与p2，起始时，都指向链表的起点A，p1每次移动1个长度，p2每次移动2个长度。如果p2在移到链表的尾端时，并未与p1相遇，表明链表中不存在环。如果p1与p2相遇在环上的某一点C，表明链表有环。

环的长度

将指针p1固定在相遇位置C，移动p2，每次移动1个长度，并用变量cnt计数。当p2再次与p1相遇时，此时cnt的值就是链表的长度。

环的起点

环的起点即图中点B，将指针p1指向链表的起始位置A，指针p2仍在位置C，指针p1与p2每次均移动一个单位，p1与p2再次相遇的位置就是环的起点位置点B。

代码

伪代码

t := &S
h := &S                 //令指针t和h均指向起始节点S。
repeat
    t := t->next
    h := h->next
    if h is not NULL       //要注意这一判断一般不能省略
        h := h->next
until t = h or h = NULL
if h != NULL             //如果存在环的話
    n := 0
    repeat                //求环的度
        t := t->next
        n := n+1
    until t = h
    t := &S               //求环的一个起点
    while t != h
    t := t->next
        h := h->next
P := *t

引用自维基百科

c++代码

#include <bits/stdc++.h>

struct Node//链表节点
{
    int data;
    Node * next;
};

bool findCircle(Node * list){
    Node* p1  = list->next, *p2;//p1移动1个单位
    bool flag;
    if(p1 == NULL){//链表只有1个节点
        return false;
    }
    p2 = p1 -> next;//p2移动两个单位
    while(p1 != p2 && p2 != NULL){
        p1 = p1->next;
        p2 = p2->next;
        if(p2 == NULL){
            break;
        }
        p2 = p2->next;//p2移动两个单位
    }
    if(p2 == NULL){
        return false;
    }
    else{
        //存在环，首先求环的长度
        int cnt = 1, p2 = p2->next;
        while(p2 != p1){
            ++cnt;
            p2 = p2->next;
        }
        //此时cnt就是环的长度

        //求环的起点
        p1 = list;
        while(p1 != p2){
            p1 = p1->next;
            p2 = p2->next;
        }
        //此时p1与p2都指向环的起点
        return true;
    }
}

简单证明

借鉴于博客上面求链表是否存在环及求环的长度的思路都很好理解，主要是为什么p1与p2再次相遇就是环的起点呢？这里假设从跑道的起始点A到环的起点B的路程为m，从B到相遇点C的路程为k，环的长度为n，相遇时乌龟的爬行路程为$S_1 = m + k + t_1 * n$，兔子的奔跑距离为$S_2 = m + k + t_2 * n(t_2 > t_1)$，兔子的速度是乌龟的两倍即$S_2 = 2 * S_1$，则$S_1 = S_2 - S_1 = (t_2 - t_1) * n$，$S_2 = 2 * (t_2 - t_1) * n$即兔子和乌龟相遇时的奔跑距离为环的整数倍，而$m + k = (t_2 - 2 * t_1) * n$也为环的整数倍。当兔子回到跑道的起始位置，乌龟从相遇点B出发时，这时，两人的速度均为单位时间内爬行1个长度，当兔子到达环的起点B即爬行了m距离时，乌龟则是k+m，此时刚好爬行环的整数倍，也处于环的起点B，即乌龟与兔子再次相遇的位置即为环的起点位置B。

复杂度分析

空间复杂度

空间复杂度为：$O(1)$。使用的p1，p2，cnt均为常量空间。

时间复杂度

假设链表中存在环，则p1移动m个长度即可到达环的起点，p2与p1间的最大距离为n-1。而p2移动速度是p1的两倍，每个单位时间内可以将其与p1的距离缩短1，则最多n-1时间，即可与p1相遇。时间复杂度为$O(m + n)$，即线性时间。

Brent的移动的兔子和传送的乌龟

简介

How do you determine if your singly-linked list has a cycle? In 1980, Brent invented an algorithm that not only worked in linear time, but required less stepping than Floyd’s Tortoise and the Hare algorithm (however it is slightly more complex). Although stepping through a ‘regular’ linked list is computationally easy, these algorithms are also used for factorization and pseudorandom number generators, linked lists are implicit and finding the next member is computationally difficult.

引用自网站 1980年，Brent提出了一种算法，不仅能在线性时间内找到环，并且使用的步数比Floyd的判圈算法要少。

算法思路

Brent’s algorithm features a moving rabbit and a stationary, then teleporting, turtle. Both turtle and rabbit start at the top of the list. The rabbit takes one step per iteration. If it is then at the same position as the stationary turtle, there is obviously a loop. If it reaches the end of the list, there is no loop. Of course, this by itself will take infinite time if there is a loop. So every once in a while, we teleport the turtle to the rabbit’s position, and let the rabbit continue moving. We start out waiting just 2 steps before teleportation, and we double that each time we move the turtle.

相比Floyd的兔子与乌龟，Brent的兔子仍然移动，但乌龟静止，达到传送时间t时，乌龟直接移动到兔子当前的位置，然后传送时间t翻倍（t = 2 * t），如此下去，如果兔子到达终点，则表示不存在环，如果兔子与乌龟相遇（兔子回到自己曾去达的位置）表示有环。

算法效率

Note that like Floyd’s Tortoise and Hare algorithm, this one runs in O(N). However you’re doing less stepping than with Floyd’s (in fact the upper bound for steps is the number you would do with Floyd’s algorithm). According to Brent’s research, his algorithm is 24-36% faster on average for implicit linked list algorithms.

兔子仍在不断移动，乌龟的传送使得其位置瞬移，缩短了它与兔子相遇时间。并且传送等待时间的不断翻倍，保证了兔子与乌龟在有限的时间内一定能相遇。

代码

伪代码

turtle = top
rabbit = top

steps_taken = 0
step_limit = 2

forever:
    if rabbit == end:
       return 'No Loop Found'
    rabbit = rabbit.next

    steps_taken += 1

    if rabbit == turtle:
        return 'Loop found'

    if steps_taken == step_limit:
        steps_taken = 0
        step_limit *= 2
        // teleport the turtle
        turtle = rabbit

引用自网站

c++代码

#include <bits/stdc++.h>

struct Node//链表节点
{
    int data;
    Node * next;
};

bool findCircle(Node * list){
    Node* p1  = list->next, *p2 = list;//p1移动1个单位
    int steps_taken = 1, step_limit = 2;
    bool flag;
    if(p1 == NULL){//链表只有1个节点
        return false;
    }

    while(p1 != p2 && p1 != NULL){
        p1 = p1->next;
        ++steps_taken;
        if(p1 == NULL){
            break;
        }
        if(steps_taken == step_limit){//达到传送时间
            steps_taken = 0;//步数清0
            step_limit = step_limit * 2;//传送时间翻倍
            p2 = p1;
        }
    }
    if(p1 == NULL){
        return false;
    }
    else{
        //存在环，首先求环的长度
        int cnt = 1, p2 = p2->next;
        while(p2 != p1){
            ++cnt;
            p2 = p2->next;
        }
        //此时cnt就是环的长度

        //求环的起点
        p1 = list;
        while(p1 != p2){
            p1 = p1->next;
            p2 = p2->next;
        }
        //此时p1与p2都指向环的起点
        return true;
    }
}