LeetCode2019第 164 场周赛

1266. 访问所有点的最小时间

题目描述

平面上有 n 个点，点的位置用整数坐标表示 points[i] = [xi, yi]。请你计算访问所有这些点需要的最小时间（以秒为单位）。 你可以按照下面的规则在平面上移动： 每一秒沿水平或者竖直方向移动一个单位长度，或者跨过对角线（可以看作在一秒内向水平和竖直方向各移动一个单位长度）。 必须按照数组中出现的顺序来访问这些点。 示例 1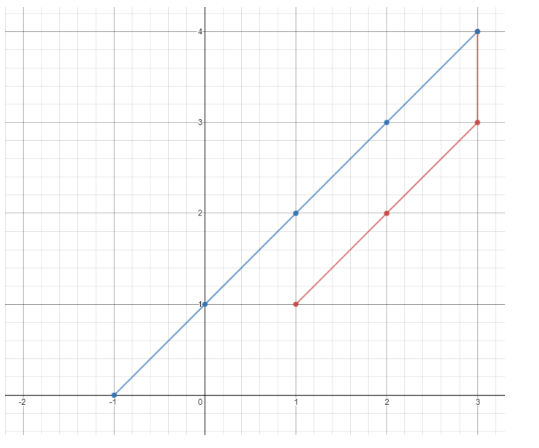： 输入：points = [[1,1],[3,4],[-1,0]] 输出：7 解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0] 从 [1,1] 到 [3,4] 需要 3 秒 从 [3,4] 到 [-1,0] 需要 4 秒 一共需要 7 秒 示例 2： 输入：points = [[3,2],[-2,2]] 输出：5 提示： points.length == n 1 <= n <= 100 points[i].length == 2 -1000 <= points[i][0], points[i][1] <= 1000

题解1

相邻两点间访问时，如果横坐标相等或者纵坐标相等，直接沿竖直方向或水平方向移动一个单位长度。如果不相等，则先沿对角线移动使横坐标或纵坐标相等，然后再水平或垂直移动。

代码1

class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int sum = 0, len = points.size();
        for(int i = 1; i < len; ++i){
            if(points[i][0] == points[i - 1][0]){//横坐标相等
                sum += abs(points[i][1] - points[i - 1][1]);
            }
            else if(points[i][1] == points[i - 1][1]){//纵坐标相等
                sum += abs(points[i][0] - points[i - 1][0]);
            }
            else{
                if(abs(points[i][0] - points[i - 1][0]) < abs(points[i][1] - points[i - 1][1])){//纵
                    sum = sum + abs(points[i][1] - points[i - 1][1]);
                }
                else{
                    sum = sum + abs(points[i][0] - points[i - 1][0]);
                }
            }
        }
        return sum;
    }
};

题解2

仔细观察代码1发现，相邻两点的访问时间等于横纵坐标差值的绝对值较大的一个。

代码2

class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int sum = 0, len = points.size();
        for(int i = 1; i < len; ++i){
            sum = sum + max(abs(points[i][0] - points[i - 1][0]), abs(points[i][1] - points[i - 1][1]));
        }
        return sum;
    }
};

1267. 统计参与通信的服务器

题目描述

这里有一幅服务器分布图，服务器的位置标识在 m * n 的整数矩阵网格 grid 中，1 表示单元格上有服务器，0 表示没有。 如果两台服务器位于同一行或者同一列，我们就认为它们之间可以进行通信。 请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。 示例 1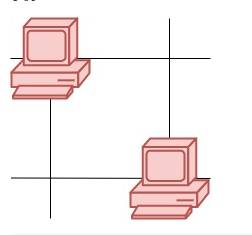： 输入：grid = [[1,0],[0,1]] 输出：0 解释：没有一台服务器能与其他服务器进行通信。 示例 2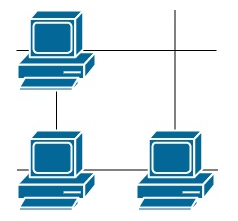： 输入：grid = [[1,0],[1,1]] 输出：3 解释：所有这些服务器都至少可以与一台别的服务器进行通信。 示例 3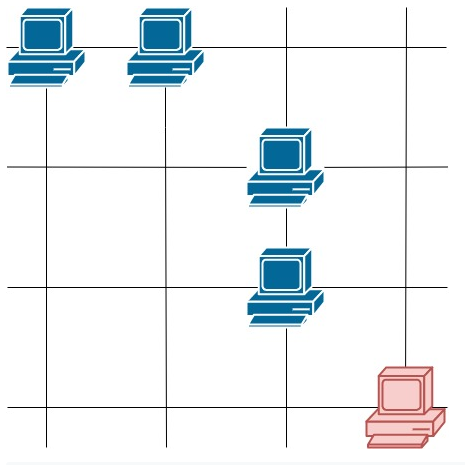： 输入：grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]] 输出：4 解释：第一行的两台服务器互相通信，第三列的两台服务器互相通信，但右下角的服务器无法与其他服务器通信。 提示： m == grid.length n == grid[i].length 1 <= m <= 250 1 <= n <= 250 grid[i][j] == 0 or 1

题解1

判断每台服务器所在行或者列除了它自己外，有没有其它的服务器，有的话表示可以通信，计数+1。否则，无法通信。

代码1

class Solution {
public:
    int countServers(vector<vector<int>>& grid) {
        int rows = grid.size(), cols = grid[0].size(), cnt = 0;
        for(int i = 0; i < rows; ++i){
            for(int j = 0; j < cols; ++j){
                if(grid[i][j]){
                    //行
                    bool flag = false;
                    for(int k = 0; k < cols; ++k){
                        if(k != j && grid[i][k]){
                            flag = true;
                            break;
                        }
                    }
                    //列
                    for(int k = 0; k < rows; ++k){
                        if(k != i && grid[k][j]){
                            flag = true;
                            break;
                        }
                    }
                    if(flag){
                        ++cnt;
                    }
                }
            }
        }
        return cnt;
    }
};

1268. 搜索推荐系统

题目描述

给你一个产品数组 products 和一个字符串 searchWord ，products 数组中每个产品都是一个字符串。 请你设计一个推荐系统，在依次输入单词 searchWord 的每一个字母后，推荐 products 数组中前缀与 searchWord 相同的最多三个产品。如果前缀相同的可推荐产品超过三个，请按字典序返回最小的三个。 请你以二维列表的形式，返回在输入 searchWord 每个字母后相应的推荐产品的列表。 示例 1： 输入：products = [“mobile”,”mouse”,”moneypot”,”monitor”,”mousepad”], searchWord = “mouse” 输出：[ [“mobile”,”moneypot”,”monitor”], [“mobile”,”moneypot”,”monitor”], [“mouse”,”mousepad”], [“mouse”,”mousepad”], [“mouse”,”mousepad”] ] 解释：按字典序排序后的产品列表是 [“mobile”,”moneypot”,”monitor”,”mouse”,”mousepad”] 输入 m 和 mo，由于所有产品的前缀都相同，所以系统返回字典序最小的三个产品 [“mobile”,”moneypot”,”monitor”] 输入 mou， mous 和 mouse 后系统都返回 [“mouse”,”mousepad”] 示例 2： 输入：products = [“havana”], searchWord = “havana” 输出：[[“havana”],[“havana”],[“havana”],[“havana”],[“havana”],[“havana”]] 示例 3： 输入：products = [“bags”,”baggage”,”banner”,”box”,”cloths”], searchWord = “bags” 输出：[[“baggage”,”bags”,”banner”],[“baggage”,”bags”,”banner”],[“baggage”,”bags”],[“bags”]] 示例 4： 输入：products = [“havana”], searchWord = “tatiana” 输出：[[],[],[],[],[],[],[]] 提示： 1 <= products.length <= 1000 1 <= products[i].length <= 2 * 10^4 products[i] 中所有的字符都是小写英文字母。 1 <= searchWord.length <= 1000 searchWord 中所有字符都是小写英文字母。

题解1

首先需将products中的字符串按照字典序排序，然后依次寻找seachWord每个字母后与之匹配的product（最多三个）。

代码1

class Solution {
public:
    vector<vector<string>> suggestedProducts(vector<string>& prod, string searchWord) {
        sort(prod.begin(), prod.end());
        vector<vector<string>>res;
        vector<string>tmp;
        for(int i = 0; i < searchWord.size(); ++i){//以每个字母前的子串进行匹配
            string s = searchWord.substr(0, i + 1);
            tmp.clear();
            int cnt = 0;
            for(int j = 0; j < prod.size(); ++j){
                if(cnt < 3 && prod[j].substr(0, i + 1) == s){//匹配且最多只能有三个
                    tmp.push_back(prod[j]);
                    ++cnt;
                }
            }
            res.push_back(tmp);
        }
        return res;
    }
};

1269. 停在原地的方案数

题目描述

有一个长度为 arrLen 的数组，开始有一个指针在索引 0 处。 每一步操作中，你可以将指针向左或向右移动 1 步，或者停在原地（指针不能被移动到数组范围外）。 给你两个整数 steps 和 arrLen ，请你计算并返回：在恰好执行 steps 次操作以后，指针仍然指向索引 0 处的方案数。 由于答案可能会很大，请返回方案数 模 10^9 + 7 后的结果。 示例 1： 输入：steps = 3, arrLen = 2 输出：4 解释：3 步后，总共有 4 种不同的方法可以停在索引 0 处。 向右，向左，不动 不动，向右，向左 向右，不动，向左 不动，不动，不动 示例 2： 输入：steps = 2, arrLen = 4 输出：2 解释：2 步后，总共有 2 种不同的方法可以停在索引 0 处。 向右，向左 不动，不动 示例 3： 输入：steps = 4, arrLen = 2 输出：8 提示： 1 <= steps <= 500 1 <= arrLen <= 10^6

题解1

如果进行dfs搜索，会超时。我们进行记忆化搜索，将已经计算过的存储下来，避免重复遍历与计算， 大大减少时间。

代码1

#define MOD (1000000007)

/*
记忆化搜索
dp[j][i] = dp[j - 1][i - 1]  + dp[j - 1][j] + dp[j - 1][i + 1]
*/

map<pair<int, int>, int>mark;
int dfs(int pos, int steps, int n){
    if(steps == 0){
        return pos == 0?1:0;
    }
    if(mark.find(make_pair(pos, steps - 1))!= mark.end()){
        mark[make_pair(pos, steps)] =  mark[make_pair(pos, steps - 1)] % MOD;
    }
   else{
       mark[make_pair(pos, steps)] = dfs(pos, steps - 1, n) % MOD;
   }
    if(pos - 1 >= 0){//左移
        if(mark.find(make_pair(pos - 1, steps - 1)) != mark.end()){
            mark[make_pair(pos, steps)] = (mark[make_pair(pos, steps)] + mark[make_pair(pos - 1, steps - 1)]) % MOD;
        }
        else{
            mark[make_pair(pos, steps)] = (mark[make_pair(pos, steps)] + dfs(pos - 1, steps - 1, n)) % MOD;
        }
    }
    if(pos + 1 < n){
        if(mark.find(make_pair(pos + 1, steps - 1)) != mark.end()){
            mark[make_pair(pos, steps)] = (mark[make_pair(pos, steps)] + mark[make_pair(pos + 1, steps - 1)]) % MOD;
        }
        else{
            mark[make_pair(pos, steps)] = (mark[make_pair(pos, steps)] + dfs(pos + 1, steps - 1, n)) % MOD;
        }
    }
    return mark[make_pair(pos, steps)];
}
class Solution {
public:

    int numWays(int steps, int arrLen) {
        mark.clear();
        return dfs(0, steps, arrLen);
    }
};

题解2

动态规划 $dp(pos, steps) = dp(pos- 1, steps - 1) + dp(pos. steps - 1) + dp(pos + 1, steps - 1)$ 其中dp(pos, steps)表示从0出发，最后经过steps步回到pos的方案数，而对于每一步有三种方案：向左移，停在原地，向右移。由此得到转移方程。

代码2

#define MOD (1000000007)

class Solution {
public:
    int numWays(int steps, int arrLen) {
        vector<vector<int>>dp(505, vector<int>(505, 0));
        dp[0][0] = 1;
        for(int i = 1; i <= steps; ++i){
            for(int j = 0; j <= min(arrLen - 1, i); ++j){
                if(j - 1 >= 0){
                    dp[j][i] = (dp[j][i] + dp[j - 1][i - 1]) % MOD; 
                }
                if(j + 1 <= i){
                    dp[j][i] = (dp[j][i] + dp[j + 1][i - 1]) % MOD;
                }
                dp[j][i] = (dp[j][i] + dp[j][i - 1]) % MOD;
            }
        }
        return dp[0][steps];
    }
};