1256. 加密数字 题目描述 给你一个非负整数 num ,返回它的「加密字符串」。 加密的过程是把一个整数用某个未知函数进行转化,你需要从下表推测出该转化函数:
题解1 我发现的规律1-2 编码位数为1位从0 - 1,3-6编码位数为2位从00 - 11。7-14编码位数为3位从000 - 111。所以从这个规律中我需要知道2个信息编码的位数及在编码中位置(即第几个)。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : string encode (int num) { long long tmp = 0 , sum = 0 , res; int bit = 0 ; string s; if (num == 0 ){ return "" ; } while (sum <= num){ if (bit == 0 ){ tmp = 1 ; } else tmp = tmp << 1 ; bit++; sum += tmp; } res = num - (sum - tmp); for (int i = 0 ; i < bit - 1 ; ++i){ s.push_back (res % 2 + '0' ); res = res >> 1 ; } reverse (s.begin (), s.end ()); return s; } };
题解2 参考圈子中的讨论,其实一个数num的编码为num+1的二进制数的低bit-1位(除去最高位)。 比如num = 6的编码为11相当于7(111)的后两位。 其实反过来题解1可以从侧面证实这种解法的正确性,最后得到的res与num存在以下关系 $latex num = res + 2^{bit - 1} - 1$变化成$latex num + 1 = res + 2^{bit - 1}$ res显然是num + 1的后bit-1位
代码2 1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : string encode (int num) { string s; int res = num + 1 ; while (res){ s.push_back ((res & 1 ) + '0' ); res = res >> 1 ; } reverse (s.begin (), s.end ()); return s.substr (1 ); } };
1257. 最小公共区域 题目描述 给你一些区域列表 regions ,每个列表的第一个区域都包含这个列表内所有其他区域。 很自然地,如果区域 X 包含区域 Y ,那么区域 X 比区域 Y 大。 给定两个区域 region1 和 region2 ,找到同时包含这两个区域的 最小 区域。 如果区域列表中 r1 包含 r2 和 r3 ,那么数据保证 r2 不会包含 r3 。 数据同样保证最小公共区域一定存在。 示例 1: 输入: regions = [[“Earth”,”North America”,”South America”], [“North America”,”United States”,”Canada”], [“United States”,”New York”,”Boston”], [“Canada”,”Ontario”,”Quebec”], [“South America”,”Brazil”]], region1 = “Quebec”, region2 = “New York” 输出:”North America” 提示: 2 <= regions.length <= 10^4 region1 != region2 所有字符串只包含英文字母和空格,且最多只有 20 个字母。
题解1 根据regions建立并查集 然后将region1与region2的所有父结点(包括它们自已)放到v1与v2中。 寻找v1与v2的第一个相交元素即为所示。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : map<string, string>maps; string findSmallestRegion (vector<vector<string>>& regions, string region1, string region2) { vector<string>v1, v2; for (int i = 0 ; i < regions.size (); ++i){ string fa = regions[i][0 ]; for (int j = 1 ; j < regions[i].size (); ++j){ maps[regions[i][j]] = fa; } } v1.push_back (region1); v2.push_back (region2); string tmp = region1; while (maps.find (tmp) != maps.end ()){ tmp = maps[tmp]; v1.push_back (tmp); } tmp = region2; while (maps.find (tmp) != maps.end ()){ tmp = maps[tmp]; v2.push_back (tmp); } for (int i = 0 ; i < v1.size (); ++i){ if (find (v2.begin (), v2.end (), v1[i]) != v2.end ()){ return v1[i]; } } return "" ; } };
1258. 近义词句子 题目描述 给你一个近义词表 synonyms 和一个句子 text , synonyms 表中是一些近义词对 ,你可以将句子 text 中每个单词用它的近义词来替换。 请你找出所有用近义词替换后的句子,按 字典序排序 后返回。 示例 1: 输入: synonyms = [[“happy”,”joy”],[“sad”,”sorrow”],[“joy”,”cheerful”]], text = “I am happy today but was sad yesterday” 输出: [“I am cheerful today but was sad yesterday”, “I am cheerful today but was sorrow yesterday”, “I am happy today but was sad yesterday”, “I am happy today but was sorrow yesterday”, “I am joy today but was sad yesterday”, “I am joy today but was sorrow yesterday”] 提示: 0 <= synonyms.length <= 10 synonyms[i].length == 2 synonyms[0] != synonyms[1] 所有单词仅包含英文字母,且长度最多为 10 。 text 最多包含 10 个单词,且单词间用单个空格分隔开。
题解1 题意比较简单,但是比较麻烦。 首先根据近义词对,将所有近义的放到同一个set中 然后将句子text转成单词数组,遍历单词,对每一个单词,在近义词中查找看是否存在近义词,如果存在,则将近义词组中的所有单词添加到v中。 最后通过DFS来生成所有近义的句子。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 vector<string>res, words; string tmp; vector<vector<string>>v (15 ); void generate (int idx, int n) if (idx >= n){ tmp.clear (); for (int i = 0 ; i < n; ++i){ if (i == 0 ){ tmp.append (words[i]); } else { tmp.append (" " ); tmp.append (words[i]); } } res.push_back (tmp); return ; } for (auto str:v[idx]){ words.push_back (str); generate (idx + 1 , n); words.pop_back (); } } class Solution {public : vector<string> generateSentences (vector<vector<string>>& sy, string text) { set<string>sets[15 ]; for (int i = 0 ; i < 15 ; ++i){ v[i].clear (); } res.clear (); words.clear (); int idx = 0 , cnt = -1 ; vector<string>sen; for (int i = 0 ; i < sy.size (); ++i){ if (i == 0 ){ ++cnt; idx =cnt; } else { idx = -1 ; for (int j = 0 ; j <= cnt; ++j){ if (sets[j].find (sy[i][0 ]) != sets[j].end () sets[j].find (sy[i][1 ]) != sets[j].end ()){ idx = j; } } if (idx == -1 ){ ++cnt; idx = cnt; } } for (auto str:sy[i]){ sets[idx].insert (str); } } istringstream s (text) ; string str; while (s >> str){ sen.push_back (str); } for (int i = 0 ; i < sen.size (); ++i){ bool flag = false ; for (int j = 0 ; j <= cnt; ++j){ if (sets[j].find (sen[i]) != sets[j].end ()){ flag = true ; for (auto iter :sets[j]){ v[i].push_back (iter); } break ; } } if (!flag){ v[i].push_back (sen[i]); } } generate (0 , sen.size ()); return res; } };
1259. 不相交的握手 题目描述 偶数 个人站成一个圆,总人数为 num_people 。每个人与除自己外的一个人握手,所以总共会有 num_people / 2 次握手。 将握手的人之间连线,请你返回连线不会相交的握手方案数。 由于结果可能会很大,请你返回答案 模 10^9+7 后的结果。 示例 1: 输入:num_people = 2 输出:1 示例 2:
题解1 这题可以用分治法也可以采用打表的形式,最多也就1000人,可以将所有的结果求出来。然后查询。 如果有n个人,g(n)记为n个握手方案的个数。编号为1, 2, 3, 4, ……, n。对于编号1,它只能和2, 4, 6, ……, 8握手,不然导致之间奇数人握手必有交叉。如果1与2握手,则3, 4, ……, n握手转成n-2个人握手问题,方案数为g(n -2)。如果1与4握手,则方案数为g(2) * g(n - 4)。 所以总方案数g(n)存在以下公式。
代码1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #define MOD (1000000000 + 7) class Solution {public : int numberOfWays (int num_people) long long res[1005 ]; memset (res, 0 , sizeof (res)); res[0 ] = res[2 ] = 1 , res[4 ] = 2 , res[6 ] = 5 ; for (int i = 8 ; i <= 1000 ; i +=2 ){ for (int j = 0 ; j < i; j += 2 ){ res[i] = (res[i] + res[j] * res[i - 2 - j]) % MOD; } } return res[num_people]; } };
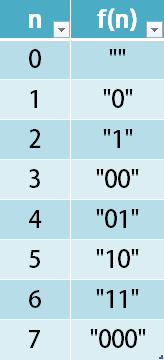 示例 1: 输入:num = 23 输出:”1000” 示例 2: 输入:num = 107 输出:”101100” 提示: 0 <= num <= 10^9
示例 1: 输入:num = 23 输出:”1000” 示例 2: 输入:num = 107 输出:”101100” 提示: 0 <= num <= 10^9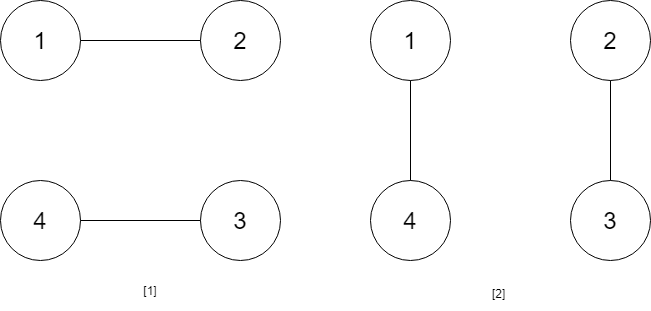 输入:num_people = 4 输出:2 解释:总共有两种方案,第一种方案是 [(1,2),(3,4)] ,第二种方案是 [(2,3),(4,1)] 。 示例 3:
输入:num_people = 4 输出:2 解释:总共有两种方案,第一种方案是 [(1,2),(3,4)] ,第二种方案是 [(2,3),(4,1)] 。 示例 3: 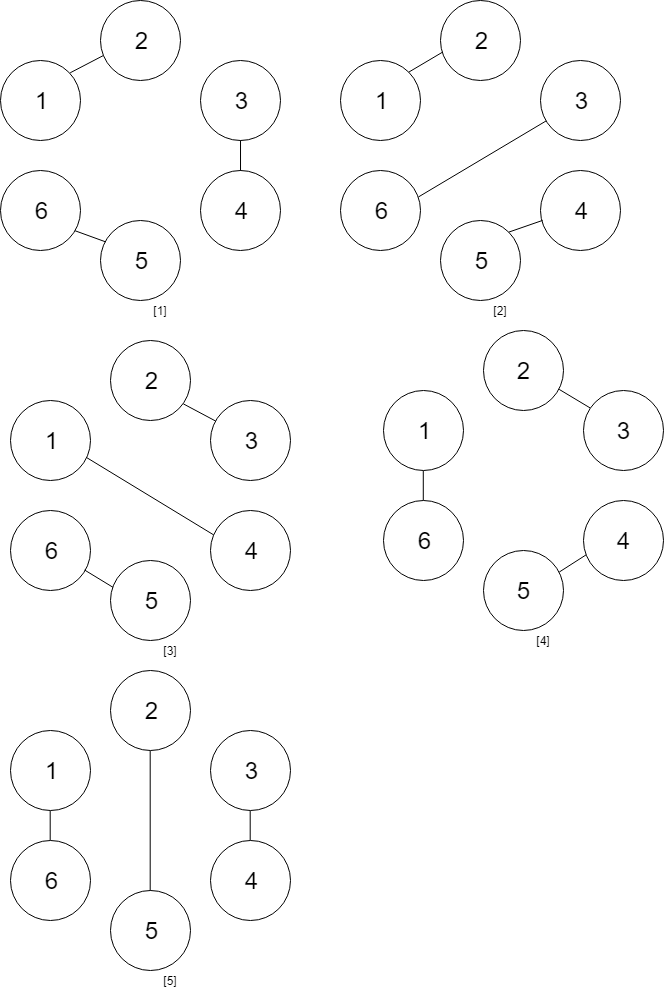 输入:num_people = 6 输出:5 示例 4: 输入:num_people = 8 输出:14 提示: 2 <= num_people <= 1000 num_people % 2 == 0
输入:num_people = 6 输出:5 示例 4: 输入:num_people = 8 输出:14 提示: 2 <= num_people <= 1000 num_people % 2 == 0